今天偶然翻阅了霍金的大设计，在第八章提到了一个生命游戏，感觉很有意思，贴在这里和大家分享下。

这个游戏是英国的数学家约翰·何顿·康威在1970年发明的，详情可以参见百度百科：http://baike.baidu.com/view/162057.htm 。这个游戏中不存在输赢，实际上，他没有玩家。它是一组制约二维宇宙的定律。这是一个决定论的宇宙，一旦设置好起始图形，定律就决定了未来有何事发生。这让我想起了一个科幻小说，具体名字不记得了，故事讲得就是未来科学家发现上帝不掷骰子，量子力学被否定，整个世界就是爱因斯坦所描述的那样有着明确的因果关系。这时男主人公通过一台能够模拟整个宇宙运行的量子计算机，设定好了宇宙大爆炸你的参数，模拟出了我们这个宇宙，并从茫茫宇宙中将地球拎出来。自此，地球的一切历史如放映机般展现在男主人公面前，从地球出生到恐龙灭绝，从夏商周到元明清，一切的一切。多么可拍的设想。

回到康威的游戏中来。这个游戏设想的世界是一个二维的棋盘，棋盘中有无限个方格。每个方格的状态只有两个：活或者死。每个方格有8个邻居。这个世界的时间是不连续的，按照离散的步骤向前发展,并遵循下面三个规律：

1. 如果活方格周围有2个或3个活邻居，它就存活。
2. 如果私房歌周围恰好有三个活邻居，它就变活。
3. 在其他的情形中，方格死去或者保持死亡状态。如果一个活方格周围有0或1个邻居，这种情况称为死于孤独；如果它有多于三个的邻居，就成为死于拥挤。

这就是游戏的全部：给定初始条件，这些定律有一代接一代的生成图形。下面接霍金《大设计》中的图，演示一下他的运行规律。

这种震荡图形称为闪光灯。

田字格式的图案在这个世界中是一个静态图案。

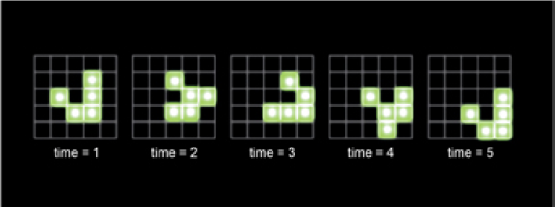
这个游戏最好玩的还是这种滑翔机图案：初始图案经过中图形变后回归到原始形态，并沿着对角线移动一个方格。滑翔机图案沿着对角线的运动称为滑翔机枪。

如果一个初始图案中包括两个或多个滑翔机图案。当它们在往后发展的过程中碰在了一起，又会发生什么样的奇异行为。

康威和他的学生创造了这个世界，是因为他们想知道具备像他们规定的那样简单的基本规则的宇宙能否包括发杂得足以自我复制的物体。在生命游戏的世界里，是否存在着这样的复合物体，它仅仅服从那个世界的定律却能在几个世代之后产生出其他的同类之物？康威和他的学生不仅能够证实这种可能性，它们甚至还证明了这样的物体在某种意义上是只能的！霍金在他的《大设计》中将这个世界比喻为“宇宙图灵机”。

写到这里我心情很激动：如果有一个游戏模拟这个这个世界，我们玩家就是这个世界里的上帝，不掷骰子！